数学化归思想举例 – 之三
程晓华
2020-10-31
4. 用已知的正方形面积求法证明勾股定理
证明勾股定理?
这在很多人眼里是不可想象的,为什么呢?
这是数学家的事情吧?
不是的,你一样可以 – 只要懂得正方形的面积怎么求即可。
我们知道,所谓的勾股定理就是指一个正三角形的垂直两边的平方的和等于斜边的平方,如下图8所示:
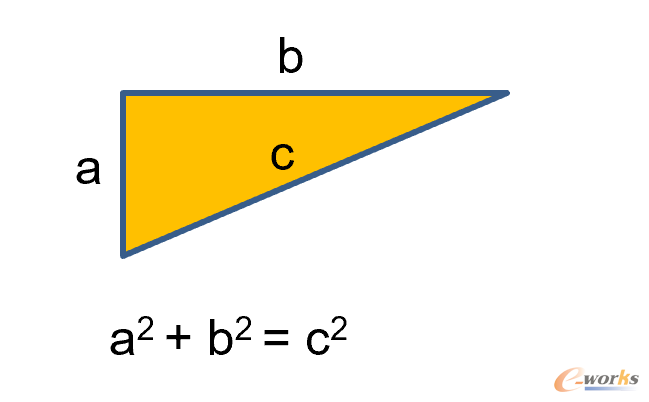
图8 勾股定理
那么,应该如何证明这个公式是正确的呢?
我们弄4个一样的这样的三角形拼在一起,如下图9所示:
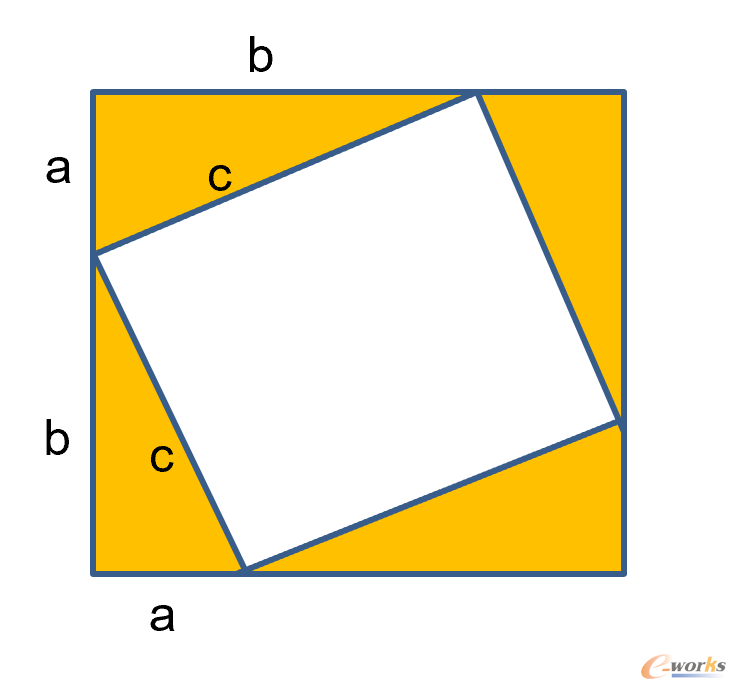
图9 4 个正三角形拼在一起
我们可以看到有内、外两个正方形,一个明显的事实是:外正方形的面积
– 内正方形的面积 = 4 个直角三角形面积,而:
①
外正方形的面积 = (a+b)2 = a2+b2
+ 2ab
②
内正方形的面积 = c2
③
4 个直角三角形面积 = 4 × ½
ab = 2ab
由于① - ② = ③,所以:
a2+b2
+ 2ab - c2 = 2ab
a2+b2 = c2
由此,我们完成了勾股定理的证明。
【关于化归思想】摘自钱珮玲《数学思想方法与中学数学(第3版)》-
化归思想方法是数学研究问题的一种基本思想方法,在处理和解决数学问题时,总的指导思想是把问题转化为能够解决的问题,这就是化归思想。
化归不仅是一种重要的解题思想,也是一种最基本的思维策略,更是一种有效的数学思维方式。
反思处理数学问题的过程和经验会发现,我们常常是将待解决的陌生问题通过转化,归结为一个比较熟悉的问题;将较难的问题通过转化,归结为一个比较容易的问题;将较繁杂的问题通过转化,归结为一个比较简单的问题来解决。因为这样就可以充分调动和运用已有的知识、经验和方法,用尽可能简单、容易的方法去解决问题。因此,从方法论的角度看,化归是使原问题归结为我们所熟悉或简单的、容易的问题。从认识论的角度看,化归思想方法是用一种联系、发展、运动变化的观点来认识问题,通过对原问题的转换,使之成为另一问题加以认识。它们的科学概括就是数学解决问题的基本思想方法-化归。
“化归”是转化和归结的简称,其基本思想是:将待解决的问题A,通过某种转化手段,归结为另一个问题B,而问题B是相对较易解决或已有固定解决程式的问题,且通过对问题B的解决可得到原问题A的解答,其中,问题B常被称作化归目标或方向,转化的手段被称为化归策略。
化归方法的哲学基础是人们对事物间的普遍联系和矛盾在一定条件下的相互转化的能动反映,它着眼于揭示联系,实现转化,通过矛盾转化解决问题。
作者程晓华(John
Cheng),全面库存管理(TIM)咨询独立顾问,《制造业库存控制技术与策略》课程创始人、讲师,《制造业库存控制技巧》、《首席物料官》、《决战库存》、《制造业全面库存管理》著作者,邮箱:johnchengbj@126.com TIM订阅号:ITOOTD
发表于:
2020-11-02 14:48 阅读(208)
评论(0) 收藏 好文推荐
本博客所有内容,若无特殊声明,皆为博主原创作品,未经博主授权,任何人不得复制、转载、摘编等任何方式进行使用和传播。
作者该类其他博文:
网站相关博文: